В даний час велика увага приділяється завданням оптимізації. В умовах обмеженості фінансових, природних та інших ресурсів вкрай гостро стоїть проблема їх економного використання. Боротьба з пробками в великих містах, розробка оптимального маршруту для перевезення вантажів з-за Уралу в Європейські регіони нашої країни, розподіл навантаження в електромережі - все це приклади завдань, де потрібне застосування методів оптимізації.
З одного боку, такі завдання вимагають акуратної постановки з точки зору фізики і техніки, з іншого - досить складних математичних методів. Рішення таких завдань школярами здається часом неможливим. Проте, в найпростіших випадках такі завдання можуть бути вирішені з використанням методів, цілком доступних і школярам старших класів.
Як правило, завдання оптимізації містять деякий функціонал, значення якого необхідно мінімізувати (або навпаки, максимізувати). Для цього в скінченномірному випадку знаходять нулі приватних похідних, в нескінченновимірних - вирішується рівняння Ейлера - Лагранжа [1]. У разі рішення таких задач школярами можна скласти комп'ютерну програму, яка б здійснювала перебір можливих значень і таким чином знаходила екстремальне значення функції. Наш досвід показує, що написання програмного коду для вирішення таких завдань не тільки доступно школярам, а й викликає у них додатковий інтерес до вивчення даної проблеми.
Ми провели зі школярами проектну роботу, яка була присвячена вирішенню важливої практичної задачі. Як відомо, у багатьох містах-«мільйонерах» є серйозні затори на дорогах. Боротися з ними можна різними способами. Один з найпопулярніших методів полягає в будівництві нових доріг. Проте, досвід показує, що це досить дорого і малоефективно. Ще один спосіб - будівництво ліній метрополітену або швидкісного трамвая. Він дуже ефективний, але теж вкрай доріг. Нарешті, досвід Москви показав, що можливий одночасно низькозатратний і високоефективний шлях, що складається в організації швидкісних маршрутів автобусів по виділених смугах. Однак, щоб такі маршрути користувалися популярністю, їх прокладка вимагає вкрай акуратних оцінок пасажиропотоку. Вирішенню цих завдань для міста Красноярська і була присвячена шкільна проектна робота. Школярами були опрацьовані кілька найбільш перспективних маршрутів, які могли б розвантажити транспортну систему даного міста.
Проведення подібних робіт вимагає від школярів знання математики в межах курсу загальної школи та вміння програмувати в рамках курсу інформатики 8 - 9 класів.
Мінімізація функцій за допомогою комп'ютера
У тому випадку, коли вирішується завдання мінімізації функції $ U (x, y, ..., z) $, в рамках вузівського курсу вона вирішується так: шукаються нулі приватних похідних: $ \ frac {\ partial U} {\ partial x} = 0, \ frac {\ partial U} {\ partial y} = 0, \ dots, \ frac {\ partial U} {\ partial z} = 0 $. Потім складається другий диференціал $ d ^ 2U $ і перевіряється, чи буде він знакоопределенной квадратичною формою [2]. Якщо ж функціонал $ U (f (x), p, q) $ містить не тільки числові параметри $ p $ і $ q $ але і невідому функцію $ f (x) $ то завдання пошуку його екстремального значення ще більше ускладнюється: наприклад, в разі якщо функціонал являє собою інтеграл, то доводиться вирішувати рівняння Ейлера - Лагранжа [1].
Всі ці методи, звичайно, є вкрай складними для школярів, особливо 8 - 9 класів. Їм невідомо, що таке приватні похідні, а визначення того, чи буде квадратична форма знакоопределенной - і зовсім непосильна праця. Однак в курсі ІКТ школярі вчаться складанню програм в рамках електронних таблиць Excel, які можна застосувати для вирішення фізичних завдань [3]. Спробуємо знайти мінімальне значення функції $ f (x) = x ^ 2-x $. Будемо заносити в стовпець A значення змінної $ x $ в стовпець B - значення функції $ f (x) $. Заповнимо стовпець А значення змінної $ x $ від 0 до 1 з кроком 0.1, а стовпець B - формулами, що виражають нашу функцію. Наприклад, в комірці B1 ми повинні записати формулу: "= A1 ^ 2 + A1". Як безпосереднє спостереження значень, отриманих у другому стовпці, так і побудований графік дозволить школярам визначити, що мінімальне значення функції знаходиться в точці $ x = 0.5 $.
Кілька більш складну задачу представляє собою знаходження мінімуму функції, що залежить від декількох змінних. У такому випадку використання таблиць Excel стає скрутним. Для цього найбільш ефективний спосіб полягає в написанні комп'ютерної програми. Вона буде перебирати всі можливі значення функції на заданій множині і знаходити найменше з них.
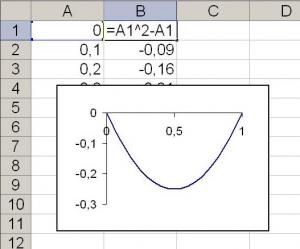
Мал. 1. Програма, написана в MS Excel для знаходження мінімуму функції, що залежить від однієї змінної.
Завдання щодо створення оптимальних автобусних маршрутів в місті Красноярську
Викладений вище метод вирішення завдань оптимізації ми застосовували для вирішення важливої практичної задачі про оптимальні інтервали для маршрутів автобуса в місті Красноярськ. Даний місто розділене річкою Єнісей на дві частини, і кожен ранок і вечір на під'їздах до мостів скупчуються пробки [5]. Передбачається використовувати досвід Москви - ввести прискорені маршрути автобусів по виділених смугах.
Нехай витрати на паливо, зарплату водія і амортизацію автобуса становлять відповідно $ a, b $ і $ c $ руб / км відповідно. (Ці дані можна визнати із загальнодоступних технічних характеристик популярних моделей, що використовуються в громадському транспорті.) Якщо довжина маршруту становить $ l $ км, а загальна кількість рейсів за час години пік дорівнює $ K $ то витрати на роботу маршруту складуть $ X = Kl ( a + b + c) $ Число рейсів можна оцінити через інтервал $ m $ наступним чином: $ K = \ frac {120} {m} $.
Оцінимо тепер доходи від маршруту. При кількості пасажирів, що дорівнює $ n $ і вартості проїзду, яка дорівнює $ q $ рублів, збір з одного автобуса складе $ \ beta = nq $ рублів. Частку $ \ gamma $ пасажирів, які скористаються маршрутом, можна оцінити так: нехай інтервал руху існуючих маршрутів буде дорівнює $ M $ а прискореного маршруту - $ m $ Тоді будемо вважати, що $ \ gamma = \ frac {Mm} {M} $ якщо загальне число пасажирів дорівнює $ P $ то збір з маршруту за годину пік складе $ Y = \ gamma q P $.
Щоб знайти оптимальні параметри, отримаємо задачу максимізації функціоналу $ U = YX $. Можна ввести залежність від декількох параметрів і знайти мінімум відповідної функції за допомогою написаної школярами програми. Приклад залежності від однієї з змінних - інтервалу m - показаний на рис. 1.
На підставі роботи даної програми нами були запропоновані наступні маршрути:
- С1 «Центральний - Кіровський», протяжність маршруту $ 2 \ times 5 $ км, оптимальний інтервал - 2 хвилини;
- С2 «Центральний - Свердловський», протяжність маршруту $ 2 \ times 13 $ км, оптимальний інтервал - 5 хвилин;
- С3 «Центральний - Ленінський», протяжність маршруту $ 2 \ times 7 $ км, оптимальний інтервал - 4 хвилини.
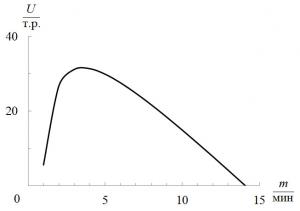
Мал. 2. Залежність прибутку від інтервалу руху для маршруту С3.
висновок
Нами було запропоновано метод вирішення завдань оптимізації школярами, який може бути заснований на застосуванні тих знань, які вони отримали в рамках шкільного курсу математики, фізики та ІКТ. Одна з практично важливих задач була вирішена нашим учнем і представлялася на Форумі Молодих Дослідників в рамках Фестивалю Науки МГУ в 2014 році.
В рамках запропонованих методів можна запропонувати і інші можливі завдання, які можуть стати основою для виконання шкільних проектно-дослідницьких робіт. Наприклад, можна запропонувати школярам самостійно запрограмувати метод найменших квадратів для обробки результатів фізичного експерименту і отримання параметрів залежності, що відрізняється від лінійної. Інший можливий варіант проектно-дослідницької роботи - обчислення оптимального маршруту для вантажів, що рухаються зі східних районів нашої країни в Центральну Росію.
Робота була виконана за підтримки програми «СТЕМ-центри» компанії Intel. Автор висловлює подяку А.С. Морозову за цінні поради та допомогу при проведенні шкільних дослідних робіт, а також колективу ГБОУ ЗОШ №96 м Москви і особливо І.М. Фатєєвої.