Obecnie wiele uwagi poświęca się problemom optymalizacji. W warunkach ograniczonych zasobów finansowych, naturalnych i innych problem ich ekonomicznego wykorzystania jest niezwykle dotkliwy. Walka z korkami w dużych miastach, rozwój optymalnej trasy transportu towarów spoza Uralu do europejskich regionów naszego kraju, rozkład obciążenia na sieć elektroenergetyczną to przykłady zadań, które wymagają zastosowania metod optymalizacji.
Z jednej strony takie zadania wymagają starannego sformułowania z punktu widzenia fizyki i technologii, z drugiej strony raczej złożonych metod matematycznych. Rozwiązanie takich problemów przez uczniów wydaje się czasami niemożliwe. Jednak w najprostszych przypadkach takie problemy można rozwiązać za pomocą metod, które są dość dostępne dla uczniów szkół średnich.
Z reguły zadania optymalizacyjne zawierają pewne funkcje, których wartość powinna być zminimalizowana (lub, przeciwnie, zmaksymalizowana). W tym przypadku, w przypadku skończonych wymiarów, znalezione są zera cząstkowych pochodnych, w nieskończonym wymiarze równanie Eulera-Lagrange'a jest rozwiązane [1]. W przypadku rozwiązywania takich problemów przez dzieci w wieku szkolnym możliwe jest stworzenie programu komputerowego, który wyliczałby możliwe wartości, a tym samym znajdowałby ekstremalną wartość funkcji. Nasze doświadczenie pokazuje, że pisanie kodu w celu rozwiązania takich problemów jest nie tylko dostępne dla studentów, ale także powoduje, że są zainteresowani studiowaniem tego problemu.
Przeprowadziliśmy prace projektowe z dziećmi w wieku szkolnym, które były poświęcone rozwiązaniu ważnego problemu praktycznego. Jak wiadomo, w wielu miastach „milionerzy” są poważnymi korkami. Możesz z nimi walczyć na różne sposoby. Jedną z najpopularniejszych metod jest budowanie nowych dróg. Doświadczenie pokazuje jednak, że jest dość kosztowne i nieskuteczne. Inny sposób - budowa linii metra lub lekkiej kolei. Jest bardzo skuteczny, ale także niezwykle drogi. Wreszcie doświadczenie Moskwy pokazało, że możliwy jest tani i wysoce wydajny sposób, polegający na organizowaniu szybkich linii autobusowych wzdłuż wyznaczonych pasów ruchu. Jednak, aby takie trasy były popularne, ich instalacja wymaga bardzo dokładnych szacunków ruchu pasażerskiego. Rozwiązanie tych problemów dla miasta Krasnojarsk i poświęcone było projektowaniu szkoły. Uczniowie opracowali kilka najbardziej obiecujących tras, które mogły rozładować system transportowy tego miasta.
Wykonanie takiej pracy wymaga od studentów znajomości matematyki w ramach ogólnego kursu szkolnego oraz umiejętności programowania w trakcie informatyki 8–9 zajęć.
Minimalizuj funkcje za pomocą komputera
W przypadku, gdy rozwiązana jest minimalizacja funkcji $ U (x, y, ..., z) $, w ramach kursu uniwersyteckiego rozwiązuje się to w następujący sposób: szukanie zer pochodnych cząstkowych: $ frac {część U} {partycja x} = 0, frac {częściowe U} {niepełne y} = 0, kropki, frak {częściowe U} {częściowe z} = 0 $. Następnie kompilowana jest druga różnica $ d ^ 2U $ i sprawdzana jest, czy będzie to postać kwadratowa określona znakiem [2]. Jeśli funkcjonalny $ U (f (x), p, q) $ zawiera nie tylko parametry numeryczne $ p $ i $ q $, ale także nieznaną funkcję $ f (x) $, to problem znalezienia jego wartości ekstremalnej jest jeszcze bardziej skomplikowany: na przykład, jeśli funkcjonalność jest całką, należy rozwiązać równanie Eulera-Lagrange'a [1].
Wszystkie te metody są oczywiście bardzo trudne dla uczniów, zwłaszcza 8 - 9 klas. Nie wiedzą, czym są pochodne cząstkowe, a określenie, czy forma kwadratowa jest określona znakiem, jest całkowicie przepracowane. Jednak na kursie ICT uczniowie uczą się tworzyć programy w arkuszach kalkulacyjnych Excel, które można wykorzystać do rozwiązywania problemów fizycznych [3]. Spróbujmy znaleźć minimalną wartość funkcji $ f (x) = x ^ 2-x $. W kolumnie A wprowadzimy wartości zmiennej $ x $ w kolumnie B - wartości funkcji $ f (x) $. Wypełnij kolumnę A wartością zmiennej $ x $ od 0 do 1 z krokiem 0,1, a kolumną B z formułami wyrażającymi naszą funkcję. Na przykład w komórce B1 musimy napisać wzór: „= A1 ^ 2 + A1”. Zarówno bezpośrednia obserwacja wartości uzyskanych w drugiej kolumnie, jak i skonstruowana fabuła pozwolą uczniom określić, że minimalna wartość funkcji jest na poziomie x $ = 0,5 $.
Nieco bardziej skomplikowanym zadaniem jest znalezienie minimum funkcji zależnej od kilku zmiennych. W takim przypadku korzystanie z tabel Excel staje się trudne. W tym celu najskuteczniejszym sposobem jest napisanie programu komputerowego. Będzie iterować po wszystkich możliwych wartościach funkcji na danym zestawie i znaleźć najmniejszą z nich.
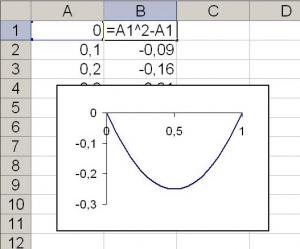
Rys. 1. Program napisany w MS Excel, aby znaleźć minimum funkcji zależnej od jednej zmiennej.
Zadanie stworzenia optymalnych tras autobusowych w mieście Krasnojarsk
Powyższa metoda rozwiązywania problemów optymalizacyjnych posłużyła do rozwiązania ważnego praktycznego problemu optymalnych przedziałów dla tras autobusowych w mieście Krasnojarsk. To miasto jest podzielone przez rzekę Jenisej na dwie części, a każdego ranka i wieczorem korki gromadzą się przy wejściach na mosty [5]. Ma wykorzystać doświadczenia Moskwy - aby wprowadzić przyspieszone trasy autobusów wzdłuż przydzielonych pasów.
Niech koszt paliwa, wynagrodzenia kierowcy i amortyzacji autobusu będą odpowiednio $ a, b $ i $ c $ rub / km. (Dane te można uzyskać z publicznie dostępnych charakterystyk technicznych popularnych modeli używanych w transporcie publicznym.) Jeśli długość trasy wynosi $ 1 $ km, a łączna liczba lotów w godzinach szczytu wynosi $ K $, koszt obsługi trasy wynosi $ X = Kl ( a + b + c) $ Liczbę lotów można oszacować za pomocą interwału $ m $ w następujący sposób: $ K = frac {120} {m} $.
Szacujemy teraz dochód z trasy. Przy liczbie pasażerów równej $ n $ i cenie równej kwocie $ q rubli, opłata za autobus wyniesie $ b = nq $ rubli. Odsetek pasażerów $ gamma, którzy wybierają trasę, można oszacować w następujący sposób: niech interwałem ruchu istniejących tras będzie $ M $, a przyspieszona trasa $ m $ Następnie zakładamy, że $ gamma = frak {Mm} {M} $ Jeśli całkowita liczba pasażerów wynosi $ P $, wówczas opłata za trasę w godzinach szczytu będzie wynosić $ Y = gamma q P $.
Aby znaleźć optymalne parametry, uzyskujemy problem maksymalizacji funkcjonalnego $ U = YX $. Możesz wprowadzić zależność od kilku parametrów i znaleźć minimum odpowiedniej funkcji za pomocą programu napisanego przez uczniów. Przykład zależności od jednej ze zmiennych, przedziału m, pokazano na ryc. 1
Na podstawie prac tego programu zaproponowaliśmy następujące trasy:
- C1 „Central - Kirovsky”, długość trasy wynosi 2 dolary za 5 $ km, optymalny odstęp to 2 minuty;
- C2 „Central - Sverdlovsk”, długość trasy wynosi 2 dolary za 13 $ km, optymalny odstęp to 5 minut;
- C3 „Central - Leninsky”, długość trasy wynosi 2 dolary za 7 $ km, optymalny odstęp to 4 minuty.
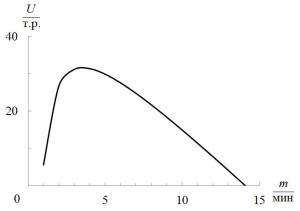
Rys. 2. Zależność zysku od przedziału ruchu dla trasy C3.
Wniosek
Zaproponowaliśmy metodę rozwiązywania problemów optymalizacyjnych przez uczniów, która może opierać się na wykorzystaniu wiedzy zdobytej w ramach kursu szkolnego z matematyki, fizyki i ICT. Jedno z ważnych zadań zostało rozwiązane przez naszego ucznia i zaprezentowane na Forum Młodych Naukowców w ramach Festiwalu Nauki Uniwersytetu Moskiewskiego w 2014 roku.
W ramach proponowanych metod można zaproponować inne możliwe zadania, które mogą stać się podstawą realizacji projektu szkolnego i prac badawczych. Na przykład można zaoferować uczniom samodzielne programowanie metody najmniejszych kwadratów w celu przetworzenia wyników eksperymentu fizycznego i uzyskania nieliniowych parametrów zależności. Inną możliwą opcją dla prac projektowych i badawczych jest obliczenie optymalnej trasy dla ładunków przemieszczających się ze wschodnich regionów naszego kraju do Rosji Centralnej.
Prace zostały przeprowadzone przy wsparciu programu Intel STEM Centers. Autor jest wdzięczny A.S. Morozow za cenne rady i pomoc w prowadzeniu badań szkolnych, a także za pracowników Moskiewskiej Państwowej Szkoły Medycznej nr 96, a zwłaszcza I.M. Fateeva.