У цяперашні час вялікая ўвага надаецца задачам аптымізацыі. Ва ўмовах абмежаванасці фінансавых, прыродных і іншых рэсурсаў вельмі востра стаіць праблема іх эканомнага выкарыстання. Барацьба з коркамі ў буйных гарадах, распрацоўка аптымальнага маршруту для перавозкі грузаў з-за Урала ў Еўрапейскія рэгіёны нашай краіны, размеркаванне нагрузкі ў электрасеткі - усё гэта прыклады задач, дзе патрабуецца прымяненне метадаў аптымізацыі.
З аднаго боку, такія задачы патрабуюць акуратнай пастаноўкі з пункту гледжання фізікі і тэхнікі, з другога - даволі складаных матэматычных метадаў. Рашэнне такіх задач школьнікамі здаецца часам немагчымым. Тым не менш, у найпростых выпадках такія задачы могуць быць вырашаны з выкарыстаннем метадаў, цалкам даступных і школьнікам старэйшых класаў.
Як правіла, задачы аптымізацыі ўтрымліваюць некаторы функцыянал, значэнне якога неабходна мінімізаваць (ці наадварот, максымізаваць). Для гэтага ў канечнамернае выпадку знаходзяць нулі прыватных вытворных, у бесконечномерном - вырашаецца раўнанне Эйлера - Лагранжа [1]. У выпадку вырашэння такіх задач школьнікамі можна скласці кампутарную праграму, якая б ажыццяўляла перабор магчымых значэнняў і такім чынам знаходзіла экстрэмальнае значэнне функцыі. Наш вопыт паказвае, што напісанне праграмнага кода для вырашэння такіх задач не толькі даступна школьнікам, але і выклікае ў іх дадатковую цікавасць да вывучэння дадзенай праблемы.
Мы правялі са школьнікамі праектную працу, якая была прысвечана вырашэнню важнай практычнай задачы. Як вядома, у многіх гарадах- «мільянерах» маюцца сур'ёзныя дарожныя коркі. Змагацца з імі можна рознымі спосабамі. Адзін з самых папулярных метадаў складаецца ў будаўніцтве новых дарог. Тым не менш, вопыт паказвае, што гэта даволі дорага і малаэфектыўна. Яшчэ адзін спосаб - будаўніцтва ліній метрапалітэна або хуткаснага трамвая. Ён вельмі эфектыўны, але таксама вельмі дарог. Нарэшце, вопыт Масквы паказаў, што магчымы адначасова нізказатратнай і высокаэфектыўны шлях, які складаецца ў арганізацыі хуткасных маршрутаў аўтобусаў па вылучаных палосах. Аднак, каб такія маршруты карысталіся папулярнасцю, іх пракладка патрабуе вельмі акуратных адзнак пасажырапатоку. Вырашэнню гэтых задач для горада Краснаярска і была прысвечана школьная праектная праца. Школьнікамі былі прапрацаваны некалькі найбольш перспектыўных маршрутаў, якія маглі б разгрузіць транспартную сістэму дадзенага горада.
Правядзенне падобных прац патрабуе ад школьнікаў веды матэматыкі ў межах курса агульнай школы і ўменні праграмаваць ў рамках курса інфарматыкі 8 - 9 класаў.
Мінімізацыя функцый з дапамогай кампутара
У тым выпадку, калі вырашаецца задача мінімізацыі функцыі $ U (x, y, ..., z) $, у рамках внузскага курсу яна вырашаецца так: шукаюцца нулі прыватных вытворных: $ \ frac {\ partial U} {\ partial x} = 0, \ frac {\ partial U} {\ partial y} = 0, \ dots, \ frac {\ partial U} {\ partial z} = 0 $. Затым складаецца другі дыферэнцыял $ d ^ 2U $ і правяраецца, ці будзе ён знакоопределенной квадратычнай формай [2]. Калі ж функцыянал $ U (f (x), p, q) $ змяшчае не толькі лікавыя параметры $ p $ і $ q $ але і невядомую функцыю $ f (x) $ то задача пошуку яго экстрэмальнага значэння яшчэ больш ускладняецца: напрыклад, у выпадку калі функцыянал ўяўляе сабой інтэграл, то прыходзіцца вырашаць раўнанне Эйлера - Лагранжа [1].
Усе гэтыя метады, вядома, з'яўляюцца вельмі складанымі для школьнікаў, асабліва 8 - 9 класаў. Ім невядома, што такое прыватныя вытворныя, а вызначэнне таго, ці будзе Квадратычным формы знакоопределенной - і зусім непасільная праца. Аднак у курсе ІКТ школьнікі вучацца складанні праграм у рамках электронных табліц Excel, якія можна ўжыць для вырашэння фізічных задач [3]. Паспрабуем знайсці мінімальнае значэнне функцыі $ f (x) = x ^ 2-x $. Будзем заносіць у слупок A значэння зменнай $ x $ ў слупок B - значэння функцыі $ f (x) $. Запоўнім слупок А значэння зменнай $ x $ ад 0 да 1 з крокам 0.1, а слупок B - формуламі, якія выказваюць нашу функцыю. Напрыклад, у вочку B1 мы павінны запісаць формулу: "= A1 ^ 2 + A1". Як непасрэднае назіранне значэнняў, атрыманых у другім слупку, так і пабудаваны графік дазволіць школьнікам вызначыць, што мінімальнае значэнне функцыі знаходзіцца ў пункце $ x = 0.5 $.
Некалькі больш складаную задачу ўяўляе сабой знаходжанне мінімуму функцыі, якая залежыць ад некалькіх зменных. У такім выпадку выкарыстанне табліц Excel становіцца цяжкім. Для гэтага найбольш эфектыўны спосаб складаецца ў напісанні кампутарнай праграмы. Яна будзе перабіраць усе магчымыя значэнні функцыі на зададзеным мностве і знаходзіць найменшае з іх.
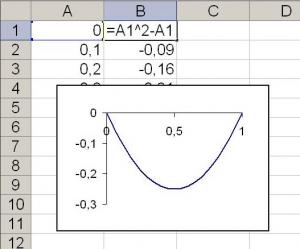
Мал. 1. Праграма, напісаная ў MS Excel для знаходжання мінімуму функцыі, якая залежыць ад адной зменнай.
Задача аб стварэнні аптымальных аўтобусных маршрутаў у горадзе Краснаярску
Выкладзены вышэй метад рашэння задач аптымізацыі мы ўжывалі для вырашэння важнай практычнай задачы аб аптымальных інтэрвалах для маршрутаў аўтобуса ў горадзе Краснаярск. Дадзены горад падзелены ракой Енісей на дзве часткі, і кожную раніцу і вечар на пад'ездах да мастам запасяцца коркі [5]. Мяркуецца выкарыстаць вопыт Масквы - увесці паскораныя маршруты аўтобусаў па вылучаных палосах.
Хай выдаткі на паліва, зарплату вадзіцеля і амартызацыю аўтобуса складаюць адпаведна $ a, b $ і $ c $ руб / км адпаведна. (Гэтыя дадзеныя магчыма даведацца з агульнадаступных тэхнічных характарыстык папулярных мадэляў, якія выкарыстоўваюцца ў грамадскім транспарце.) Калі працягласць маршруту складае $ l $ км, а агульная колькасць рэйсаў за час гадзіны пік роўна $ K $ то выдаткі на працу маршруту складуць $ X = Kl ( a + b + c) $ Лік рэйсаў можна ацаніць праз інтэрвал $ m $ наступным чынам: $ K = \ frac {120} {m} $.
Ацэнім цяпер даходы ад маршруту. Пры колькасці пасажыраў, роўным $ n $ і кошту праезду, роўнай $ q $ рублёў, збор з аднаго аўтобуса складзе $ \ beta = nq $ рублёў. Долю $ \ gamma $ пасажыраў, якія скарыстаюцца маршрутам, можна ацаніць так: хай інтэрвал руху існуючых маршрутаў будзе роўны $ M $ а паскоранага маршруту - $ m $ Тады будзем меркаваць, што $ \ gamma = \ frac {Mm} {M} $ Калі агульная колькасць пасажыраў роўна $ P $ то збор з маршруту за гадзіну пік складзе $ Y = \ gamma q P $.
Каб знайсці аптымальныя параметры, атрымаем задачу максімізацыі функцыяналу $ U = YX $. Можна ўвесці залежнасць ад некалькіх параметраў і знайсці мінімум адпаведнай функцыі пры дапамозе напісанай школьнікамі праграмы. Прыклад залежнасці ад адной з зменных - інтэрвалу m - паказаны на мал. 1.
На падставе працы дадзенай праграмы намі былі прапанаваны наступныя маршруты:
- С1 «Цэнтральны - Кіраўскі», працягласць маршруту $ 2 \ times 5 $ км, аптымальны інтэрвал - 2 хвіліны;
- С2 «Цэнтральны - Свярдлоўскі», працягласць маршруту $ 2 \ times 13 $ км, аптымальны інтэрвал - 5 хвілін;
- С3 «Цэнтральны - Ленінскі», працягласць маршруту $ 2 \ times 7 $ км, аптымальны інтэрвал - 4 хвіліны.
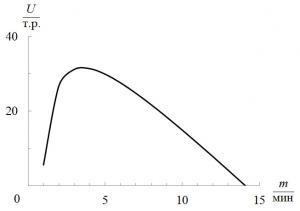
Мал. 2. Залежнасць прыбытку ад інтэрвалу руху для маршруту С3.
заключэнне
Намі было прапанаваны метад рашэння задач аптымізацыі школьнікамі, які можа быць заснаваны на ўжыванні тых ведаў, якія яны атрымалі ў рамках школьнага курса матэматыкі, фізікі і ІКТ. Адна з практычна важных задач была вырашана нашым вучнем і ўяўлялася на Форуме Маладых Даследчыкаў ў рамках Фестывалю Навукі МДУ ў 2014 годзе.
У рамках прапанаваных метадаў можна прапанаваць і іншыя магчымыя задачы, якія могуць стаць асновай для выканання школьных праектна-даследчых работ. Напрыклад, можна прапанаваць школьнікам самастойна запраграмаваць метад найменшых квадратаў для апрацоўкі вынікаў фізічнага эксперыменту і атрымання параметраў залежнасці, якая адрозніваецца ад лінейнай. Іншы магчымы варыянт праектна-даследчай працы - вылічэнне аптымальнага маршруту для грузаў, якія рухаюцца з усходніх раёнаў нашай краіны ў Цэнтральную Расію.
Праца была выкананая пры падтрымцы праграмы «СТЕМ-цэнтры» кампаніі Intel. Аўтар выказвае падзяку А.С. Марозаву за каштоўныя парады і дапамогу пры правядзенні школьных даследчых работ, а таксама калектыву ГБОУ САШ №96 г. Масквы і ў асаблівасці І.М. Фатеева.